Some useful probability distributions

In this section we will explore two useful probability distributions using R.

Note

It's good to get used to visualising these in R. But if you prefer you can also use the interactive distribution zoo site to explore these distributions.

Note on learning outcomes

For this part of CM4, we are focussed on the concepts. You don't need to know all the mathematical details of these distributions, nor do you need to know all the R-specific details below. On the other hand, you should have a sense of what they are used to represent and why we might be interested in them, their shape and how the parameters work.

The Normal distribution

The normal distribution, also known as the gaussian distribution, is commonly used to handle variables that might be sums of lots of other things.

For example, we might imagine that the expression of a gene depends on lots of factors that determine expression levels, all of which add up to the eventual expression level. Or we might imagine that a phenotype (like height, for example) is determined by lots of genetic and environmental factors all adding up. It turns out that variable that are sums of lots of small things like this tend to be normal.

A famous demonstration of this is the so-called 'Galton board' which you can see here:

Galton board video

The result of adding up all those random jumps to the left and right is... a normal distribution.

Challenge

Pick a mean value $\mu$ (start somewhere between $-10$ and $10$) and a variance $v$ (which must be positive - for example, $2$ is a good starting choice). Then plot the density of the normal distribution over the continuous range $x=-20 \cdots 20$.

The normal distribution density in R is given by the dnorm() function.

For example, you could plot it by creating a grid of values to plot at:

x = seq( from = -20, to = 20, by = 0.001 )

and choosing a mean and variance parameter:

mu = 5
variance = 2

Then use the dnorm() function to plot:

plot(
    x,
    dnorm(x, mean = mu, sd = sqrt( variance )),
    type = 'l',
    lwd = 2,
    xlab = "x",
    ylab = "Normal distribution density",
    xlim = c( -20, 20 ),
    ylim = c( 0, 0.4 ),
    bty = 'n'
)
grid()

Note. As I've done above, it is best to set sensible xlim and ylim values.

How does the distribution differ as you vary the mean and the variance?

For reference, here is the formula for the normal distribution density:

$$x|\mu,v \sim \frac{1}{\sqrt{2\pi v}}\cdot e^{\frac{1}{2}\frac{(x-\mu)^2}{v}}$$

It's not as complicated as it looks - the first bit $\left(\frac{1}{\sqrt{2\pi v}}\right)$ is just the normalising constant (it doesn't depend on $x$ and is just there to make the distribution sum to $1$. The second part is more or less just a quadratic formula depending on the squared distance of $x$ to the mean $\frac{(x-\mu)^2}{v}$. (You don't need to know these details for the exam.)

Binomial distribution

The binomial distribution answers the following important question:

Suppose a particular allele $A$ is at frequency $p$ in a population of interest. If we sample $n$ chromosomes and genotype them, how many will carry the allele?

Challenge

Pick a number of samples n (start between 5 and 20) and a probability or frequency $p$ (start between 0.1 and 0.9).

Then plot the binomial distribution over the range of integers $x = 0, 1, 2, \cdots, n$.

For example, you could pick parameters like this:

n = 20
p = 0.1

and use dbinom() to plot it

x = 0:n
binom = dbinom( x, size = n, prob = p )
names(binom) = x
barplot(binom)

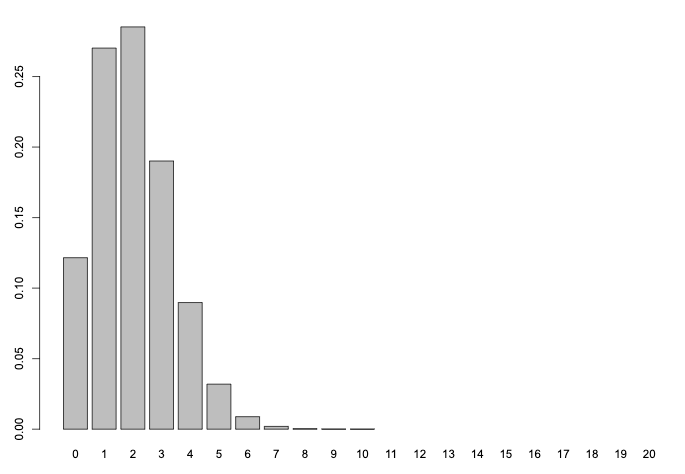
Question How does the shape of the binomial differ as you vary $n$ and $p$?

Note. The plot above for $n=20$ and $p=0.1$ says that - if the true frequency was $10$ and we sampled $20$ chromosomes, we'd be most likely to find $2$ that carry the allele - but it could be as high as, say, $6$.

On the other hand - we'd be very unlikely to find as many as $10$ alleles. This can be computed using the corresponding pbinom() function:

pbinom(
    q = 10,
    size = n,
    prob = p,
    lower.tail = F # mass under `dbinom()` under the right-hand tail
)